La hipérbola.
Las hipérbolas son secciones cónicas formadas cuando un plano interseca a un par de conos.
Se dice que una hipérbola es el lugar geométrico de los puntos del plano \(P(x,\ y)\) tales que el valor absoluto de la diferencia de distancias a dos puntos fijos llamados focos es constante. Se excluye en la definición la posibilidad de que el punto esté sobre la recta que une los focos.
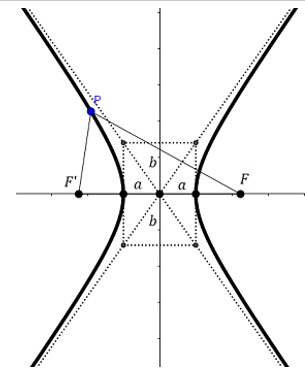
El eje que contiene los focos se denomina eje focal siendo la distancia entre los focos es igual a dos veces un parámetro llamado \(c,~~(2c)\). El eje focal interseca la hipérbola en dos puntos llamados vértices, la distancia entre estos puntos de cortes es llamada eje transverso y su valor es dos veces un parámetro llamado "\(a\)" tal que \(a< c.\) El segmento de recta normal al eje focal en el centro hipérbola de longitud \(2b\) tal que \(c^2=a^2+b^2\) se denomina eje conjugado Un segmento que une dos puntos de la hipérbola es llamado cuerda y una cuerda que pasa por un foco es llamada cuerda focal, si la cuerda es normal al foco se llama lado recto, como existen dos focos también existen dos lados rectos al igual que en la elipse un segmento que une un punto de la hipérbola y uno de sus focos es llamado radio vector. A diferencia de la elipse no existe la restricción a>b así que \(b\) puede ser mayor que \(a\).
Ecuaciones de la hipérbola.
Considere una hipérbola cualquiera cuyos focos y centro se encuentran sobre una recta horizontal, donde el centro (punto medio entre los focos) es el punto \((h,k)\) y los focos son los puntos \(F(h-c,k)\) y \(F^\prime(h+c,k)\) de la definición de hipérbola se cumple que,
$$\left|d\left(P,F\right)-d\left(P,F^\prime\right)\right|=cte$$
Llamando a esta constante \(cte=2a\) por conveniencia para el manejo algebraico, la ecuación anterior se puede escribir como,
$$\left|d\left(P,F\right)-d\left(P,F^\prime\right)\right|=2a$$
De la definición de valor absoluto la expresión anterior produce para un punto \(P(x,y)\),
$$\left\{\begin{array}i
d(P,F)-d(P,F')=2a\\
d(P,F)-d(P,F')=-2a\end{array}\right.$$
la primera expresión se cumple cuando el punto \(P(x,y)\) se ubica a la izquierda del centro y la segunda cuando está a la derecha. Aplicando la fórmula de la distancia entre dos puntos a estas expresiones se tiene,
$$\left\{\begin{array}i
\sqrt{(x-h+c)^2+(y-k)^2}-\sqrt{(x-h-c)^2+(y-k)^2}=2a\\
\sqrt{(x-h+c)^2+(y-k)^2}-\sqrt{(x-h-c)^2+(y-k)^2}=-2a
\end{array}\right.$$
Desarrollando la primera expresión de las anteriores,
\begin{align}
&\sqrt{{(x-h+c)}^2+{(y-k)}^2}=2a+\sqrt{{(x-h-c)}^2+{(y-k)}^2}\\
&\left(x-h+c\right)^2+\left(y-k\right)^2 =4a^2+4a\sqrt{{(x-h-c)}^2+{(y-k)}^2}+{(x-h-c)}^2+{(y-k)}^2\\
&\left(x-h+c\right)^2-{(x-h-c)}^2=4a^2+4a\sqrt{{(x-h-c)}^2+{(y-k)}^2}\\
&4cx-4ch-4a^2=4a\sqrt{{(x-h-c)}^2+{(y-k)}^2}\\
&4c(x-h)-4a^2=4a\sqrt{{(x-h-c)}^2+{(y-k)}^2}\\
&c(x-h)-a^2=a\sqrt{{(x-h-c)}^2+{(y-k)}^2}\\
&c^2{(x-h)}^2-2c(x-h)a^2+a^4=a^2({(x-h-c)}^2+{(y-k)}^2)\\
&c^2{(x-h)}^2-2c(x-h)a^2+a^4=a^2({(x-h)}^2-2c(x-h)a^2+c^2+{(y-k)}^2)\\
&c^2{(x-h)}^2+a^4=a^2{(x-h)}^2+a^2c^2+a^2{(y-k)}^2\\
&(c^2-a^2){(x-h)}^2-a^2{(y-k)}^2=a^2c^2-a^4\\
&(c^2-a^2){(x-h)}^2-a^2{(y-k)}^2=a^2(c^2-a^2)\end{align}
Como \(c>a\) la cantidad \(c^2-a^2>0\) y es llamada \(b^2\) de donde se tiene, primera forma canónica de la hipérbola,
$$b^2{(x-h)}^2-a^2{(y-k)}^2=a^2b^2$$
que al dividir todo por \(a^2b^2\) se transforma en la segunda forma canónica de la hipérbola,
$$\frac{{(x-h)}^2}{a^2}-\frac{{(y-k)}^2}{b^2}=1$$
La cual es la expresión para la hipérbola con centro en el punto \((h,k)\) y eje transverso horizontal.
Segunda forma canónica de la hipérbola con centro en \((h,k)\)
$$\frac{{(x-h)}^2}{a^2}-\frac{{(y-k)}^2}{b^2}=1\ \ \ ó \ \ \ \frac{{(y-k)}^2}{a^2}-\frac{{(x-h)}^2}{b^2}=1$$La segunda expresión aplica cuando el eje transverso es vertical y se deduce al desarrollar, $$\sqrt{{(x-h)}^2+{(y-k+c)}^2}-\sqrt{{(x-h)}^2+{(y-k-c)}^2}=2a$$
Asíntotas de una hipérbola.
Observe nuevamente la figura del inicio de la sección note que se forma un rectángulo cuyo centro es el centro de la hipérbola y que por este punto pasan dos rectas que contienen las diagonales del rectángulo, observe detenidamente lo que pasa con la función a medida que \(x\) tiende al infinito (crece sin límite) o a menos infinitos (decrece sin límite) la función adopta un comportamiento asintótico para ambas rectas (se acerca se acerca, pero no la toca). Si en la primera forma canónica de la hipérbola se despeja ye se tiene, \begin{align} &b^2{(x-h)}^2-a^2{(y-k)}^2=a^2b^2\\ &a^2{(y-k)}^2=b^2{(x-h)}^2-a^2b^2\\ &\left(y-k\right)^2=\frac{b^2}{a^2}\left(\left(x-h\right)^2-a^2\right)\\ &y=\pm\frac{b}{a}\sqrt{\left(x-h\right)^2-a^2}+k\\ &y=\pm\frac{b}{a}\sqrt{\left(x-h\right)^2\left(1-\frac{a^2}{\left(x-h\right)^2}\right)}+k\\ &y=\pm\frac{b}{a}(x-h)\sqrt{1-\frac{a^2}{\left(x-h\right)^2}}+k \end{align} Si observa la cantidad debajo del signo radical notará que si \(x\) aumenta su valor sin límite la cantidad sud radical tiende a uno y de esto queda la expresión para la , asíntotas de hipérbola de eje focal horizontal $$y=\frac{b}{a}(x-h)+k\ \ \ \ \ \ \ \ \ \ \ \ \ y=-\frac{b}{a}(x-h)+k$$ Mediante un procediendo análogo se demuestra que las asíntotas de hipérbola de eje focal vertical están dadas por $$y=\frac{a}{b}(x-h)+k\ \ \ \ \ \ \ \ \ \ \ \ \ y=-\frac{a}{b}(x-h)+k$$ Si en \(b^2\left(x-h\right)^2-a^2\left(y-k\right)^2=a^2b^2\) el centro \((h,k)=(0,0)\) la expresión se transforma en \(b^2x^2-a^2y^2=a^2b^2\) y las asíntotas de la hipérbola se pueden obtener mediante la expresión \(b^2x^2-a^2y^2=0,\) de donde $$\left(ax+by\right)\left(ax-by\right)=0$$ que al resolver cada factor se obtienen las rectas de la asíntotas, $$y=\frac{b}{a}x\ \ \ \ \ \ \ \ \ \ \ \ \ \ y=-\frac{b}{a}$$
Excentricidad de la hipérbola.
Al igual que en la elipse la hipérbola tiene una excentricidad \(e=c/a\) que por ser \(c>a,\) entonces \(e>1.\)
El siguiente cuadro resumen muestra los elementos más importantes a tener en cuenta al estudiar la hipérbola.
\begin{array}{c |c |c |c |c |c}{}
{\rm Ecuación}& {\rm Centro } &{\rm Focos} &{\rm Vertices} &{\rm Eje transverso} &{\rm Asíntotas}\\
\hline \frac{{(x-h)}^2}{a^2}-\frac{{(y-k)}^2}{b^2}=1
& (h,k)& (h\pm c,k)&(h\pm a\ ,k) &{\rm eje~} x &y=\pm\frac{b}{a}(x-h)+k\\
\hline \frac{{(y-k)}^2}{a^2}-\frac{{(x-h)}^2}{b^2}=1&(h,k)&(h,\ k\pm c)&(h,k\pm a)&{\rm eje~}y&y=\pm\frac{a}{b}(x-h)+k
\end{array}
En un primer momento se pueden usar los resultados del cuadro para escribir las respuestas relacionadas a una hipérbola, aunque no se recomienda la memorización de este cuadro sino más bien usar el razonamiento analítico para determinar cada uno de los elementos.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
tab-2
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
tab-15
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Una hipérbola por definición. Determinar la ecuación general del lugar geométrico de los puntos\( P\left(x,y\right)\) tales que el valor absoluto de la diferencia de sus distancias a los puntos fijos \(A\left(1,\ 5\right)\) y \(B(1,\ -5)\) sea igual a \(6.\)
Hipérbolas centradas en el origen. Determinar el centro, focos vértices y las asíntotas de las hipérbolas siguientes. $$1.\ \frac{x^2}{3}-\frac{y^2}{2}=1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2.\ \frac{y^2}{2}-\frac{x^2}{3}=1$$
Construyendo la ecuación de una hipérbola Los focos y los vértices de una hipérbola son los puntos: \(F(5,\ 0),~~F’(-5,\ 0),~~V(14,\ 0)\) y \(V_2(-4,\ 0)\) respectivamente. Determine la ecuación de la hipérbola. Dibujar su gráfica e indicar las asíntotas.
Determinando elementos de una hipérbola. Dada la ecuación de la hipérbola \(7y^2-11x^2=77\) determine las coordenadas de los focos, de los vértices, ecuaciones de las asíntotas.
Determinar las coordenadas de los vértices, focos y ecuaciones de las asíntotas de la hipérbola con centro en \(C(3,\ 3)\), cuyos focos están sobre la recta \(y=5\), si se sabe que la distancia entre los focos es \(10\) unidades y la distancia entre sus vértices es \(8\) unidades.
Completando el \(t.c.p.\) para una hipérbola Dada la ecuación \(25x^2-4y^2-250x-24y+489=0.\) Determinar su forma canónica, excentricidad, vertices y focos.
Completando el \(t.c.p.\) para una hipérbola Dada la ecuación \(5y^2-7x^2+14x+40y+38=0.\) Determinar su forma canónica, excentricidad, focos y vertices.
